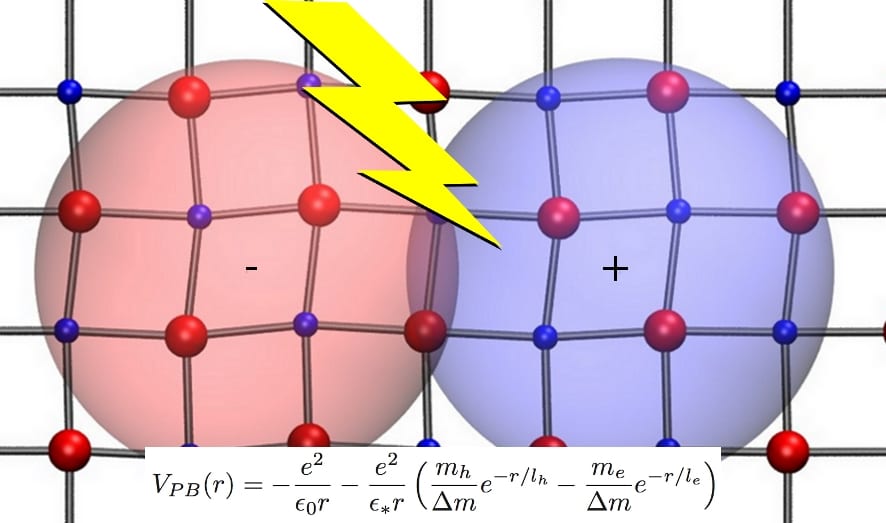
Excitons are often the lowest energy excitation created by light absorption in semiconductors. An exciton in a semiconductor is understood as an electron-hole pair that attracts each other by the electric Coulomb interaction. In many cases, the Schröndiger equation of this excited state is analogous to that of the hydrogen atom, but the electron and the hole have effective masses due to the underlying crystal periodic potential. Moreover, the Coulomb interaction is reduced by a factor equal to the dielectric constant, which arises from the many-body nature of the electronic system. This model is known as the Wannier-Mott exciton.
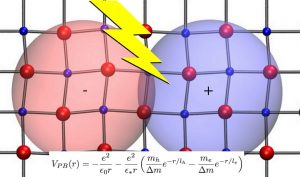Methyl-ammonium lead tri-iodide is a hybrid organic-inorganic perovskite that has revolutionized the photovoltaic research, allowing solar cell prototypes with record efficiencies over 20 %. One of its singular properties is to have an extremely polarizable lattice that augments significantly the screening of the electron-hole interaction. A problem is that the Wannier-Mott model predicts two different exciton binding energies if the dielectric constant includes either the electronic plus lattice screening (~2 meV) or only the electronic screening (~50 meV). Moreover, experimental determination of the binding energies provides very different values (~16 meV).
Menendez-Proupin, Beltran Rios and Wahnon have shown a mechanism by which the optical phonons can modify the electron-hole interaction and explain the exciton binding energy determined in experiments. They applied a field-theory formalism, by which the wavefunction of an exciton coupled with the quantized phonon field is transformed in the wavefunction of a pure exciton bound with a distance-dependent dielectric function. This model was rigorously developed in the seventies for excitons in binary semiconductors having one single optical phonon branch without dispersion. Here, the model shows its usefulness with these complex metal-halide perovskites. Remarkably, none of the physical parameters of the model was fitted, but were obtained from first-principles calculations.
This text is kindly provided by Eduardo Menendez Proupin
