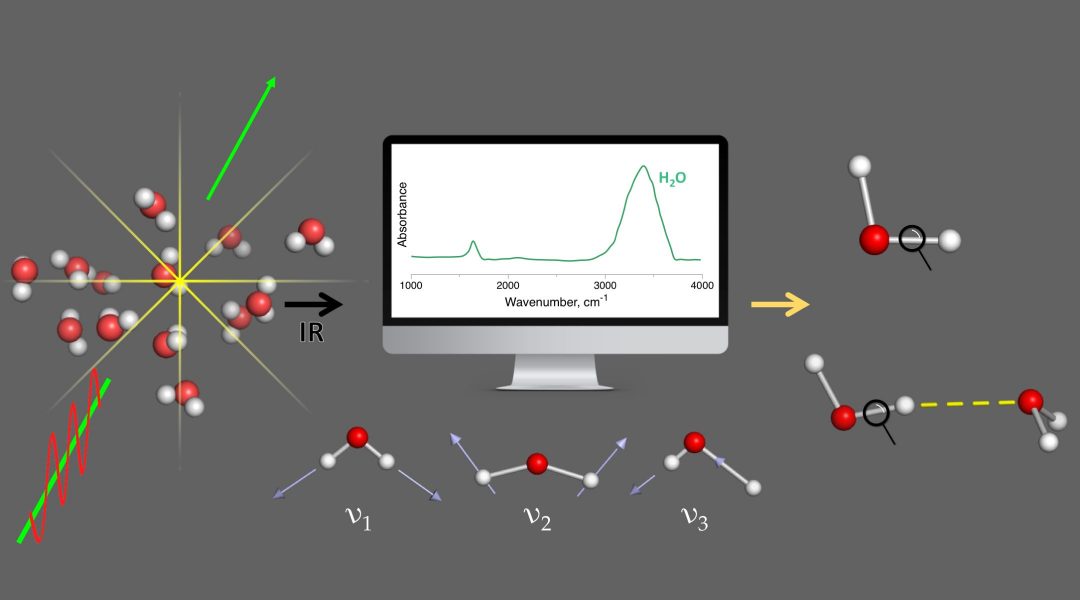
Vibrational spectroscopy is an indispensable tool in almost all branches of chemical sciences nowadays. Besides exploring molecular structure by identifying signature peaks associated with various functional groups, vibrational spectra are frequently used to monitor chemical bond strength changes with red- (weakening) or blue-shifting (strengthening).
The idea of characterizing chemical bond strength with vibrations dates back to the 1930s, when Richard Badger discovered an inverse power relationship (Badger’s rule) between bond length and vibrational force constant for a series of diatomic molecules.
However, in general, Badger’s original rule does not apply to polyatomic molecules. Fundamental molecular vibrations are typically delocalized over the whole molecule rather than being localized at individual chemical bonds, because of electronic and mass coupling. McKean could isolate some C–H/O–H stretching vibrations via isotopic substitution, and Henry and others examined the fifth overtones of molecules with X–H bonds (X = O, N, C) and observed one band for each unique X–H bond.
In a review published in WIREs Computational Molecular Science, Dr. Elfi Kraka of Southern Methodist University in Dallas, Texas, and her colleagues discuss how the local vibrational mode theory, originally developed by Konkoli and Cremer in 1998, offers a generally applicable solution to characterize any chemical bond in a molecule based on fundamental normal vibrational modes theory.
Local vibrational modes can be conveniently calculated with modern quantum chemical packages within the harmonic approximation. They are obtained by solving vibrational mass-decoupled Euler-Lagrange equations (i.e., they rest on a physically sound framework).
“A local vibration mode associated with a chemical bond can be understood as a vibration where all atomic masses except those of the two atoms forming the bond are zero, so that the remaining atoms of the molecule can effortlessly follow this local motion,” explained Dr. Kraka. “By slowly turning on the masses, mass coupling develops towards full strength, and the local modes smoothly transform into their normal mode counterparts. This important one-to-one correspondence allows for a unique decomposition of normal modes into local mode contributions, leading to a detailed analysis of an IR/Raman spectrum.”
Local vibrational modes have been successfully applied to characterize covalent bonding and weak chemical interactions ranging from hydrogen to tetrel bonding — a bond between an electron-donating group and a group 14 element acting as a Lewis acid. A number of new electronic parameters and descriptors have been derived, such as a new aromaticity, leading to a renewed understanding of Clar’s rule, and the long-searched-for extension of Badger’s rule to polyatomic molecules.
Some highlights include the identification of the first B–H…p interaction in iridium-dimercapto-carborane complexes; the development of a new quantitative measure of metal–ligand bonding to replace the Tolman electronic parameter, called the metal–ligand electronic parameter; and the first atomistic explanation of why warm water freezes faster than cold water, an effect known in the literature as the “Mpemba Effect” — named after its discovery by Mpemba in 1969.
“Although proposed more than two decades ago, the local vibrational mode theory is still thriving,” said Kraka. “Recently, we managed to extend the local vibrational mode theory from isolated molecules to periodic systems, a big step forward. Besides serving as a new powerful tool for the analysis of bonding in crystals, a systematic comparison of the bond strength in periodic systems and in isolated molecules becomes possible, allowing for the direct monitoring of structure and bonding changes upon crystallization.
Our vision is that both experimental and computational spectroscopists will routinely apply the local mode analysis in the future, enriching our chemical knowledge.”
Written by: Elfi Kraka, Wenli Zou, and Yunwen Tao
Reference: Elfi Krafka, et al. ‘Decoding chemical information from vibrational spectroscopy data: Local vibrational mode theory,’ WIREs Computational Molecular Science (2020). DOI: 10.1002/wcms.1480