Modeling and simulations are used for the optimization of manufacturing processes and the evaluation of component performance under loading in service. Accuracy of such simulations depends on the accuracy of the constitutive laws used to describe material behavior. These laws are generally anisotropic and sensitive to the crystal structure and internal microstructure of the material.

To ease computational expense, however, simple phenomenological constitutive laws are commonly employed in the simulation tools, such as finite elements. They neglect microstructure and its evolution and anisotropy. As a result, they can be insufficient in describing accurately the mechanical behavior of many metals that exhibit anisotropic strain hardening. Reliable simulation tools that incorporate the dominant micro-scale deformation processes, such as dislocation slip, twinning, and martensitic transformations, into constitutive laws can potentially overcome this problem.

In their eview article in Advanced Engineering Materials, Marko Knezevic and Irene J. Beyerlein emphasize the importance of the physics-based plasticity theory in constitutive material descriptions for more accurate simulations of deformation in the development of metal forming processes, for controlling mechanical behavior via tailoring microstructural features, and for subsequent component performance testing.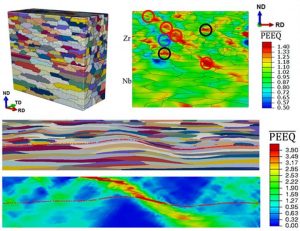

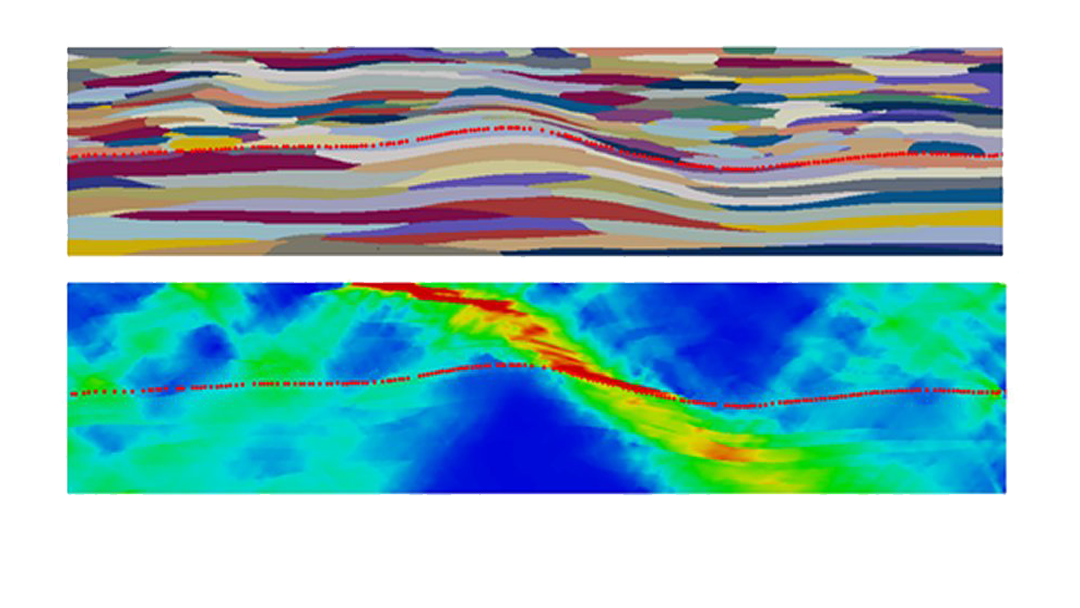
In particular, it reviews recent advances in the development of a model for the critical activation stresses for thermally activated glide and the expansion of deformation twins, its implementation into meso-scale polycrystal plasticity models, and several applications for predicting the constitutive response of polycrystalline metals at the macro-scale within implicit finite element framework. Calculations are performed for a broad range of polycrystalline metals, differing in microstructural complexity and crystal structure.

The examples include face-centered cubic metals like AA6022-T4, IN718, Haynes 25, and pure Cu; body-centered cubic metals like Nb, Ta, Ta-10W, and steel DP590; and hexagonal close-packed metals like pure Be, pure Zr, pure Ti, AZ31, Mg4Li; and finally orthorhombic U. Excellent agreement with experimental measurement is demonstrated in terms of the texture, stress-strain response, and geometrical samples changes that occur during deformation.