Dopants are widely used in materials science and play critical roles in a wide variety of applications, for example, in the fabrication of P- or N-type semiconductors. The properties of doped materials can depend on the conditions (temperature, etc.) of the doping process, and different characteristics of a material can be attributed to the atomic arrangement of the dopant.
Atomic resolution holography techniques, including X-ray fluorescence, photoelectron, and neutron holography, provide new insight into the local atomic structures of dopants.
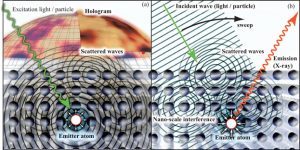
Three-dimensional (3D) atomic images can be reconstructed from atomic resolution holograms using reconstruction calculation techniques—the development of appropriate algorithms being a critical first step in the reconstruction process.
An algorithm based on Fourier transformation (Barton’s method) has been proposed, which is effective for volume, or multiple-energy, holograms. This is because relevant information is preserved in the Fourier transform, which is required to reconstruct the 3D image.
Reconstruction of an image from a single-energy hologram is difficult and can hardly be applied to photoelectron holography, as a phase shift is induced in the scattered wave and its wave function cannot be described using simple trigonometric functions. To overcome this limitation, Tomohiro Matsushita from the Japan Synchrotron Radiation Research Institute (JASRI) has presented details of an algorithm developed on the basis of an iterative approach with L1-regularized linear regression and a modified steepest descent method. This article is part of a recently published Special Issue on Synchrotron Radiation: Progress of Data Analysis,Data-Driven Science, and Theory for Science in physica status solidi (b) – basic solid state physics, guest edited by Shinya Hosokawa and László Pusztai.
Kindly contributed by the Authors.

















