Toroidal moments, first introduced by Y. B. Zel’Dovich in 1958, are key elements for realizing a number of interesting phenomena such as non-radiating charge-current configurations and non-reciprocal refraction of light backward waves.

A particularly interesting feature of a stationary toroidal moment is that the associated electric and magnetic fields vanish in the far field. Still the vector potential is finite. Phase-sensitive quantities of a quantum system, however, react to a vector potential, even in the absence of fields, making toroidal moments an attractive tool to couple to such systems in a non-invasive way.

In the work published in Advanced Quantum Technologies, Dr. Jonas Wätzel and Professor Jamal Berakdar of Martin-Luther University Halle-Wittenberg, Germany, go a step further and show how to trigger ultrafast toroidal electronic distribution on the nanoscale, which offers a spatio-temporal quantum phase probe. A generic case for a charge-current distribution generating a toroidal moment is that of a polar classical current density on the surface of a torus (marked green in the Figure).

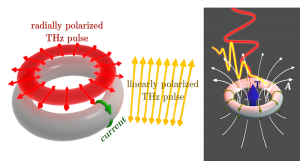
To trigger a homogeneous, unidirectional polar charge current, two time‐delayed THz pulses are applied.

To accomplish such a quantum mechanical charge distribution on the nanoscale, a donut shape quantum structure is irradiated by two pulses, picoseconds apart: a linearly polarized THz pulse (yellow arrows) and a time-delayed few cycles, radially-polarized THz pulse (red arrows).

The research team showed that using this method, a steady-state toroidal moment (blue arrow marked T) builds up as swiftly as the pulse duration. A nearby object does not experience electric nor magnetic fields but feels the photo-generated vector potential (field lines of the vector potential A are indicated white). This was in fact demonstrated explicitly in the study.

“The time structure of the driving THz pulses can be designed accurately, which allows launching picosecond trains of vector potentials,” says Professor Berakdar. “Technically, the toroidal moment is for other quantum objects a gauge-invariant vector potential”.

Quantum structures such as the Josephson junctions and persistent currents are susceptible to such potentials. Another important application is to employ the generated toroidal moment directly to toroidal materials. In this case, the launched toroidal moment couples directly to the sample’s order parameter thus offering a new spatio-temporal tool to access and steer the topologically protected toroidal ordering.